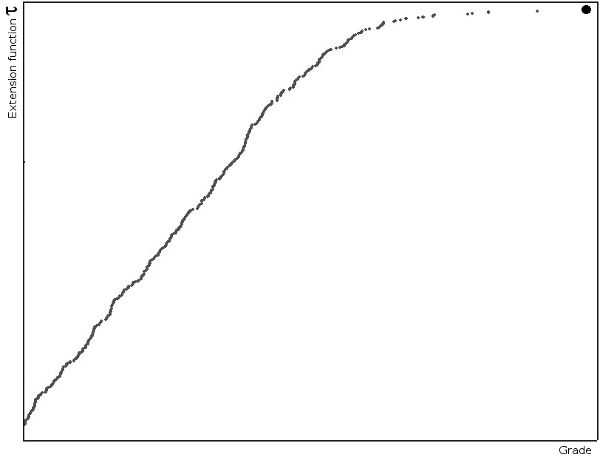
Figure 1 represents a cumulative frequency of a topographic variable V obtained from 470 samples in Walker Lake (see Isaac and Srivastava) picked randomly from a very large region. This cumulative frequency is standardized so the values range from 0 to 1.

Can the y-axis be called a cumulative conditional distribution function (CCDF)? Remember that a distribution function is the other name of probability function, so each point of the CCDF represents a cumulative probability.

Although in many books and papers this kind of graphic is assumed as the representation of a CCDF function, the answer is NO!

Let´s remember some fundamentals of Geostatistics:

A random variable is a variable whose values are randomly generated according to some probabilistic mechanism (Isaac and Srivastava). For example: if the values are independent one from each other, like the outcomes obtained by throwing a dice several times, and the probability for each outcome is always the same, then there is a unique probability function for all the possible outcomes: it represents the mechanism associated to this random variable.

If a variogram of a variable produces a pure nugget effect, then there is just one probability function associated to the variable, and the variable is a random variable: the probability of getting a certain value for a sample do not depend from which part of the deposit it was taken.

A random function is a set of random variables that have some spatial locations and whose dependence on each other is specified by some probabilistic mechanism (Isaac and Srivastava). This is the case of the V variable of Walker Lake. As the samples are located far away one from the other, each sample is associated to a different random variable, and each of them has its own CCDF, its own probability function. These random variables are not independent and are associated to the others by a probabilistic mechanism. For example, a variogram is a model for a random function.

Figure 1, the y-axis represents an extension function as it can be seen in the description of the Field Parametric Geostatistics theory, but never a CCDF.

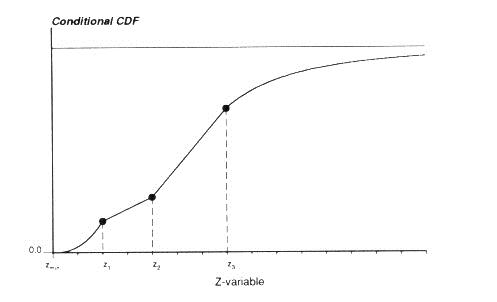
Figure 2 is taken from GSLib book, edited  1992, page 132. In the book, the values in the y-axis are taken as CCDF values. Following the definitions of random variable and random function it is clear that the y-axis cannot be called a CCDF axis. It can be a cumulative frequency graphic, declustered or not, or an extension function, like in the V variable graphic represented in Figure 1, but never a CCDF.

This conceptual error is very common even in consecrated books.

Fig. 1
Cumulative frequency of a topographic variable V obtained from 470 samples in Walker Lake.

Fig. 2
Taken from GSLib book (1992), page 132.